पारस्परिकता (विद्युत नेटवर्क)

विद्युत नेटवर्क के सन्दर्भ में पारस्परिकता (reciprocity) परिपथ का एक गुण है जो परिपथ के दो बिन्दुओं पर वोल्टता और धारा के परस्पर सम्बन्ध के बारे में है। पारस्परिकता प्रमेय के अनुसार, किसी परिपथ के किसी एक बिन्दु पर लगाये गये वोल्टता स्रोत के कारण उसी परिपथ के किसी दूसरे बिन्दु जो धारा बहती है, उतनी ही धारा पहले बिन्दु पर बहेगी यदि उस वोल्टता स्रोत को दूसरे बिन्दु पर लगाया जाय। पारस्परिकता प्रमेय उन सभी परिपथों में लागू होता है जो रैखिक (linear) हैं और जिनके अवयव समय के साथ अपरिवर्तनशील हैं। इसके अलावा उसमें कोई दूसरा स्वतन्त्र स्रोत या परतन्त्र स्रोत (dependent source) नहीं होना चाहिये। विद्युत नेटवर्क से सम्बन्धित पारस्परिकता प्रमेय, अपने अधिक व्यापक रूप विद्युतचुम्बकत्व में पारस्परिकता (reciprocity in electromagnetism) का एक विशेष रूप है।

माना कि पोर्ट A में धारा ${\displaystyle I_{\text{A}}}$ डाली जाती है तो पोर्ट B पर वोल्टेज ${\displaystyle V_{\text{B}}}$ पैदा होती है। अब यदि पोर्ट B में धारा ${\displaystyle I_{\text{A}}}$ डालने पर पोर्ट A पर वोल्टेज ${\displaystyle V_{\text{B}}}$ उत्पन्न हो तो यह नेटवर्क पारस्परिक नेटवर्क कहलायेगा। इसी तरह, पारस्परिकता की द्वैत स्थिति से भी परिभाषित किया जा सकता है। पोर्ट A पर वोल्टेज ${\displaystyle V_{\text{A}}}$लगाने पर पोर्ट बी पर धारा ${\displaystyle I_{\text{B}}}$ उत्पन्न हो तथा पोर्ट B पर वोल्टेज ${\displaystyle V_{\text{A}}}$ लगाने पर पोर्ट A पर धारा ${\displaystyle I_{\text{B}}}$ उत्पन्न हो तो यह परिपथ, पारस्परिक परिपथ है।

कोई भी नेटवर्क जिसमें केवल आदर्श संधारित्र, प्रेरकत्व ( पारस्परिक प्रेरकत्व सहित), और प्रतिरोध हों, अर्थात जिसमें केवल रैखिक और द्विपक्षीय (Bilateral) अवयव ही लगे हों, वह पारस्परिकता का गुण प्रदर्शित करेगा।^[1]

कुछ नेटवर्क अपारस्परिक होते हैं या जानबूझकर अपारस्परिक गुणों से युक्त बनाये जाते हैं। किसी नेटवर्क में कोई लौहचुम्बकीय युक्ति लगी हो (जैसे लौहचुम्बकीय क्रोड वाला प्रेरकत्व) तो इस नेटवर्क के अ-पारस्परिक होने की सम्भावना होती है क्योंकि लौहचुम्बकीय युक्तियाँ अरैखीय हो सकतीं हैं। परिसंचारी (सर्कुलेटर) और आइसोलेटर आदि ऐसी युक्तियाँ हैं जिन्हें जानबूझकर अ-पारस्परिकता के गुण से युक्त बनाया जाता है, और अपारस्परिकता का यह गुण यहाँ उनकी उपयोगिकता का मुख्य कारण भी है। ^[2]

किसी पारस्परिक नेटवर्क के ट्रान्सफर फलन को जेड-पैरामीटर, वाई-पैरामीटर, या एस-पैरामीटर मैट्रिक्स के रूप में लिखा जाय तो यह मैट्रिक्स मुख्य विकर्ण के दोनों ओर सममित (सिमेट्रिकल) होती है। अर्थात् ये मैट्रिक्स यदि गैर-सममित हों तो इसका अर्थ यह है कि यह नेटवर्क अ-पारस्परिक नेटवर्क है। यह भी ध्यातव्य है कि सममित मैट्रिक्स होने का अर्थ यह नहीं है कि सम्बन्धित नेटवर्क सममित होगा। ^[3]

किसी नेटवर्क को h-पैरामीटर के रूप में अभिव्यक्त करने पर यदि ${\displaystyle h_{12}=-h_{21}}$ हो तो वह पारस्परिक होगा। ABCD पैरामीटर के रूप में अभिव्यक्त नेटवर्क में यदि ${\displaystyle AD-BC=1}$ हो तो वह पारस्परिक होगा।

पारस्परिकता को निम्नलिखित नेटवर्क के माध्यम से समझाया जा सकता है। यह केवल प्रतिरोधों से निर्मित एक क्षीणकारी (attenuator) है। इसको देखने से ही पता चलता है कि यह सममित नेटवर्क नहीं है। फिर भी यह पारस्परिकता का गुण प्रदर्शित करेगा क्योंकि यह एक रैखिक द्विपक्षीय नेटवर्क है।

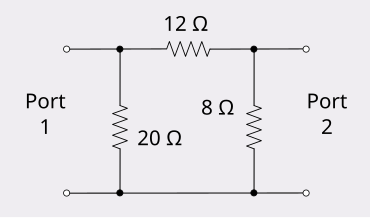
माना कि इसके पोर्ट 1 में 6 A धारा डालते हैं। गणना करके निकाल सकते हैं कि इससे पोर्ट 2 पर 24 V पैदा होगा।

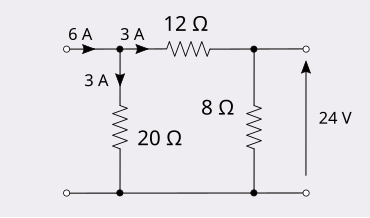
अब यदि पोर्ट 2 में 6 A धारा डाली जाय, तो पोर्ट 1 पर 24 वोल्ट पैदा होगा (चित्र के अनुसार गणना करके देखें)।

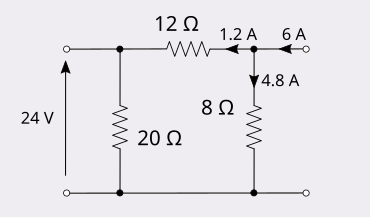
यह होना ही था क्योंकि हमे पता है कि यह पारस्परिक नेटवर्क है।

इस उदहरण में, जिस पोर्ट से धारा नहीं डाली जा रही है, उसे खुला (ओपेन) छोड़ते हुए गणना करनी है (मानो कि वहाँ वोल्टमीटर लगा हुआ है)।

दूसरी तरफ, यदि किसी नेटवर्क में एक पोर्ट पर वोल्टेज लगाकर दूसरे पर धारा की गणना करनी है, तो दूसरे पोर्ट को शॉर्ट करना आवशयक होता है (मानो कि वहा अमीटर लगा हुआ है)।