समद्विभाजन विधि

संख्यात्मक विश्लेषण के क्षेत्र में, समद्विभाजन विधि (Bisection method) अरैखिक समीकरण का मूल निकालने की एक संख्यात्मक विधि है। यह एक पुनरावृत्‍तिमूलक विधि (इटरेटिव मेथड) है।

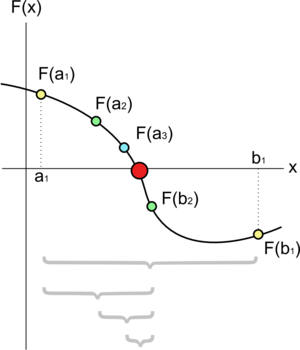
समद्विभाजन विधि समीकरण f(x) = 0 के वास्तविक मूल निकालने के लिये प्रयुक्त होती है। यदि यह फलन अन्तराल [a, b] में सतत हो और f(a) तथा f(b) के चिह्न विपरीत हों तो a और b को मूल का 'ब्रैकेट' कहते हैं क्योंकि मूल इसी बीच में कहीं होगा।

प्रत्येक चरण में इस विधि में मूल-अन्तराल का मध्य बिन्दु c = (a+b) / 2 निकाला जाता है। फिर f(c) का मान निकालते हैं। यदि, f(c) = 0 तो c ही समीकरण का मूल है किन्तु ऐसा होने की सम्भावना बहुत कम होती है। अब यदि f(a) और f(c) के चिह्न परस्पर विपरीत हैं तो मूल का ब्रैकेट [a, c] होगा अन्यथा [b, c] होगा।

इस प्रकार बार-बार मूल का ब्रैकेट आधा करते हुए अन्ततः मूल के अत्यधिक निकट पहुँच जाते हैं और गणना रोक दी जाती है।

माना कि समद्विभाजन विधि से निम्नलिखित समीकरण का मूल निकालना है-

${\displaystyle f(x)=x^{3}-x-2\,.}$

सबसे पहले हमें दो संख्याएँ ${\displaystyle a}$ और ${\displaystyle b}$ ढ़ूढना है ताकि ${\displaystyle f(a)}$ तथा ${\displaystyle f(b)}$ के मानों का चिह्न एक दूसरे के उल्टा हो। इस फलन के लिये, ${\displaystyle a=1}$ तथा ${\displaystyle b=2}$ इस शर्त को पूरा करते हैं क्योंकि,

${\displaystyle f(1)=(1)^{3}-(1)-2=-2}$ (ऋण चिह्न)

तथा

${\displaystyle f(2)=(2)^{3}-(2)-2=+4\,.}$ (धन चिह्न)

चूँकि फलन सतत है, इसलिये मूल अन्तराल [1, 2] के बीच में कहीं होगा।

अब इस अन्तराल का मध्य बिन्दु निकालते हैं:

${\displaystyle c_{1}={\frac {2+1}{2}}=1.5}$

इस बिन्दु पर फलन का मान है : ${\displaystyle f(c_{1})=(1.5)^{3}-(1.5)-2=-0.125}$. यह मान ऋणात्मक है। इसका अर्थ यह हुआ कि मूल अन्तराल [1.5, 2] के बीच में होगा। इसी तरह करते जाने पर मूल को घेरने वाला अन्तराल निरन्तर कम होता जायेगा। इसे निम्नांकित सारणी में दिखाया गया है।

Iteration	${\displaystyle a_{n}}$	${\displaystyle b_{n}}$	${\displaystyle c_{n}}$	${\displaystyle f(c_{n})}$
1	1	2	1.5	−0.125
2	1.5	2	1.75	1.6093750
3	1.5	1.75	1.625	0.6660156
4	1.5	1.625	1.5625	0.2521973
5	1.5	1.5625	1.5312500	0.0591125
6	1.5	1.5312500	1.5156250	−0.0340538
7	1.5156250	1.5312500	1.5234375	0.0122504
8	1.5156250	1.5234375	1.5195313	−0.0109712
9	1.5195313	1.5234375	1.5214844	0.0006222
10	1.5195313	1.5214844	1.5205078	−0.0051789
11	1.5205078	1.5214844	1.5209961	−0.0022794
12	1.5209961	1.5214844	1.5212402	−0.0008289
13	1.5212402	1.5214844	1.5213623	−0.0001034
14	1.5213623	1.5214844	1.5214233	0.0002594
15	1.5213623	1.5214233	1.5213928	0.0000780

13 आवृत्तियों के बाद स्पष्ततः मूल लगभग 1.521 पर कन्वर्ज होता दिख रहा है।

• मिथ्या स्थिति विधि
• छेदिका विधि
• न्यूटन की विधि