मॉड्युलर गणित

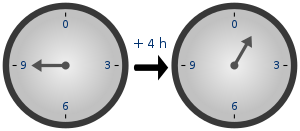
मॉड्युलर गणित पूर्णाकों के गणित की एक प्रणाली है जिसमें किसी पूर्णांक पर पहुँचने के बाद गिनती १ से शुरू हो जाती है। इसे कभी-कभी घड़ी का गणित भी कहते हैं।

इस क्षेत्र में स्विस गणितज्ञ आयलर ने बहुत उल्लेखनीय कार्य किया। इसके बाद कार्ल फ्रेडरिक गाउस ने इसको और आगे बढ़ाया।

मोड्युलो गणित का एक छोटा सा उपयोग घड़ियाँ के समय में होता है। अभी सुबह के ८ बजे हैं ; अब से ७ घण्टे बाद ८ + ७ = १५ बजना चाहिए जिसे हम ३ बजना कहते हैं। (१५ - १२ = ३)। अर्थात् मॉड्युलो १२ के लिए १५ और ३ दोनो समान हैं।

दो पूर्ण संख्याओं a और b (धन, ऋण या शून्य) को मापांक n (modulo n) के प्रति समशेष (congruent) कहते हैं, जब n से a - b विभाज्य है। इसको निम्नलिखित प्रकार से लिखते हैं :

${\displaystyle a\equiv b{\pmod {n}},\,}$

n को समशेषता का मापांक (modulus) कहते हैं।

उदाहरण के लिए

${\displaystyle 38\equiv 14{\pmod {12}}\,}$

क्योंकि 38 − 14 = 24, जो  12 का गुणज है।

ऋणात्मक पूर्णांकों के लिए भी यही नियम है-

${\displaystyle -8\equiv 7{\pmod {5}}.\,}$

${\displaystyle 2\equiv -3{\pmod {5}}.\,}$

${\displaystyle -3\equiv -8{\pmod {5}}.\,}$

समशेषता के गुणधर्म समीकरणों के गुणधर्मों के समान हैं।

यदि a ${\displaystyle \equiv }$ b (mod m) और c ${\displaystyle \equiv }$ d (mod m), तब a+c ${\displaystyle \equiv }$ b+d (mod m) और ac ${\displaystyle \equiv }$ bd (mod m)।

यदि x का एक बहुपदीय फलन f (x) हैं, जिसें x के गुणक पूर्णांक हैं और a ${\displaystyle \equiv }$ b (mod m), तो f (a) ${\displaystyle \equiv }$ f (b) (mod m), परंतु यदि ab ${\displaystyle \equiv }$ ac (mod m), तो यह आवश्यक नहीं है कि b ${\displaystyle \equiv }$ c (mod m), उदाहरणार्थ 1 ${\displaystyle \equiv }$ 6 (mod 4), परंतु १ और ३ समशेष नहीं हैं (mod 4) के प्रति।

ab ${\displaystyle \equiv }$ ac (mod m) से जो उचित फल निकाला जा सकता है, वह केवल यही है कि समशेषता की इस अंकन पद्धति (notation) का एक बड़ा लाभ यह है कि इसकी सहायता से संख्या सिद्धांत के बहुत से फलों (results) को सुंदर ढंग से निरूपित किया जा सकता है।

संपूर्ण और लघुकृत अवशेषों का समुच्चय (Complete and Reduced Residue Sets) - समशेषता संबंध तुल्यता संबंध है। इसका अर्थ है कि निम्नाकित संबंध सत्य है :

(१) a ${\displaystyle \equiv }$ a (mod m) ;

(२) a ${\displaystyle \equiv }$ b (mod m) का अर्थ b ${\displaystyle \equiv }$ a (mod m) है।

(३) a ${\displaystyle \equiv }$ b (mod m), b ${\displaystyle \equiv }$ c (mod m) का अर्थ a ${\displaystyle \equiv }$ c (mod m) है।

इसलिए समशेषता संबंध पूर्णाकों (integers) के समुच्चय को अतुल्यता के वर्गों में इस प्रकार बाँटता है कि एक वर्ग के प्रत्येक दो पूर्णांक मापक m के प्रति समशेष हैं और भिन्न भिन्न वर्गों के दो पूर्णांक मापक m के प्रति समशेष नहीं हैं। यदि m वर्गों में से प्रत्येक वर्ग से एक एक पूर्णांक लिया जाए, तो मापांक m के प्रति संपूर्ण अवशेषों का एक एक समुच्चय प्राप्त होगा। इस प्रकार -३, ३, २, १२, १४, २०, -६ मापांक ७ के प्रति संपूर्ण अवशेषों का समुच्चय है। मापांक m के प्रति सरलतम अवशेषी का समुच्चय (१) ०, १, २, ३... m-१ है और (२) निरपेक्ष लघुतम संपूर्ण अवशेषों का अमुच्चय निम्नांकित है :

0, ${\displaystyle \equiv }$ 1, ${\displaystyle \equiv }$ 2,...... ${\displaystyle \equiv }$ (m-1)/2, जब m विषम है

तथा 0, ${\displaystyle \equiv }$ 1, ${\displaystyle \equiv }$ 2,.... ${\displaystyle \equiv }$ (m-2)/2, जब m सम है

इसी प्रकार यदि m के प्रति अभाज्य पूर्णांकों का समुच्चय लिया जाए, तो वे f (m) तुल्यता के ऐसे वर्गों में बँट सकते हैं कि किसी एक वर्ग की प्रत्येक २ संख्याएँ मापांक m के प्रति समशेष होंगी और भिन्न भिन्न वर्गों की कोई २ संख्याएँ मापांक m के प्रति समशेष नहीं हैं। पहले की भाँति यदि प्रत्येक वर्ग से एक संख्या ली जाए, तो मापांक m के प्रति लघुकृत अवशेषों का एक समुच्चय प्राप्त होता है। m = १२ के लिए इस प्रकार का एक समुच्चय १, ५, ७, ११ है।

यह स्मरणीय है कि यदि मापांक m के संपूर्ण अवशेषों के समुच्चय अवयवों को m के सापेक्ष किसी अभाज्य संख्या r से गुण किया जाए, तो मापांक m के प्रति संपूर्ण अवशेषों का एक दूसरा समुच्चय प्राप्त होता है। इसी प्रकार यदि मापांक m के प्रति लघुकृत अवशेषों के समुच्चय के सभी अवयवों को m के सापेक्ष किसी अभाज्य संख्या m से गुणा किया जाए, तो मापांक m के प्रति लघुकृत अवशेषों का एक दूसरा वर्ग प्राप्त होगा। इससे निम्नांकित आयलर फेर्मा (Euler-Fermat) प्रमेय प्राप्त है :

rf(m) ${\displaystyle \equiv }$ १ (mod m), यदि (r, m) = १

• संख्या सिद्धान्त

• In this modular art article, one can learn more about applications of modular arithmetic in art.
• An article on modular arithmetic on the GIMPS wiki
• Modular Arithmetic and patterns in addition and multiplication tables
• Whitney Music Box—an audio/video demonstration of integer modular math
• Automated modular arithmetic theorem provers:
  • Spear
  • AAProver—Simple C++ framework easy to use in other applications, supporting (among others) all integer operators present in languages such as C/C++/Java and arbitrary bit-width.