Figure 1: Example two-port network with symbol definitions. Notice the port condition is satisfied: the same current flows into each port as leaves that port. द्वि-प्रद्वार जालक्रम (टू-पोर्ट नेटवर्क) ऐसे विद्युत परिपथ को कहते हैं जिसमें बाहरी जगत (नेटवरक) से जुड़ने के लिये दो-जोड़ी (अर्थात, चार) सिरे होते हैं। उदाहरण के लिये ट्रान्जिस्टर एक द्वि-पोर्ट नेटवर्क है (यद्यपि इसमें चार नहीं तीन ही सिरे होते हैं। एक सिरा इनपुट और आउटपुट दोनों प्रद्वारों में उभयनिष्ट (कॉमन) होता है।)
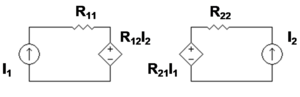
द्वि-प्रद्वार का z-तुल्य निरुपण जिसमें I1 और I2 स्वतन्त्र चर हैं। यद्यपि इस चित्र में प्रतिरोध दिखाये गये हैं किन्तु उनके स्थान पर प्रतिबाधा समझिए। [ V 1 V 2 ] = [ z 11 z 12 z 21 z 22 ] [ I 1 I 2 ] {\displaystyle \left[{\begin{array}{c}V_{1}\\V_{2}\end{array}}\right]=\left[{\begin{array}{cc}z_{11}&z_{12}\\z_{21}&z_{22}\end{array}}\right]\left[{\begin{array}{c}I_{1}\\I_{2}\end{array}}\right]} z 11 = V 1 I 1 | I 2 = 0 z 12 = V 1 I 2 | I 1 = 0 {\displaystyle z_{11}={V_{1} \over I_{1}}{\bigg |}_{I_{2}=0}\qquad z_{12}={V_{1} \over I_{2}}{\bigg |}_{I_{1}=0}} z 21 = V 2 I 1 | I 2 = 0 z 22 = V 2 I 2 | I 1 = 0 {\displaystyle z_{21}={V_{2} \over I_{1}}{\bigg |}_{I_{2}=0}\qquad z_{22}={V_{2} \over I_{2}}{\bigg |}_{I_{1}=0}} ध्यान दें कि सभी Z प्राचलों की विमा (डिमेन्शन) ओम है।
सामने लिखे समीकरणों का Y-तुल्य निरूपण जिसमें V1 और V2 स्वतन्त्र चर हैं। [ I 1 I 2 ] = [ y 11 y 12 y 21 y 22 ] [ V 1 V 2 ] {\displaystyle \left[{\begin{array}{c}I_{1}\\I_{2}\end{array}}\right]=\left[{\begin{array}{cc}y_{11}&y_{12}\\y_{21}&y_{22}\end{array}}\right]\left[{\begin{array}{c}V_{1}\\V_{2}\end{array}}\right]} जहाँ
y 11 = I 1 V 1 | V 2 = 0 y 12 = I 1 V 2 | V 1 = 0 {\displaystyle y_{11}={I_{1} \over V_{1}}{\bigg |}_{V_{2}=0}\qquad y_{12}={I_{1} \over V_{2}}{\bigg |}_{V_{1}=0}} y 21 = I 2 V 1 | V 2 = 0 y 22 = I 2 V 2 | V 1 = 0 {\displaystyle y_{21}={I_{2} \over V_{1}}{\bigg |}_{V_{2}=0}\qquad y_{22}={I_{2} \over V_{2}}{\bigg |}_{V_{1}=0}} यदि y 12 = y 21 {\displaystyle y_{12}=y_{21}} व्युत्क्रम द्वि-प्रद्वार (reciprocal two port) कहते हैं। कोई भी नेटवर्क जिसमें केवल रैखिक प्रतिरोध , प्रेरकत्व तथा संधारित्र हों - व्युत्क्रम नेटवर्क होगा। यह ध्यान रखना चाहिए कि ऐसे अवयव भी होते हैं जो पैसिव तो हैं किन्तु ब्युत्क्रम नहीं। उदाहरण के लिए सर्कुलेटर और आइसोलेटर दोनों पैसिव नेटवर्क हैं व्युत्क्रम नहीं हैं (ये दोनों बड़े उपयोगी हैं)। किसी अवयव में लौहचुम्बकीय पदार्थ का उपयोग किया गया हो तो सम्भवतः वह व्युत्क्रम नहीं होगा।
यह भी ध्यान दें कि सभी Y प्राचलों की विमा , सीमेन्स (siemens) है।
सामने लिखे समीकरणों का H-तुल्य प्राचलों के साथ निरूपण जिसमें I1 और V2 स्वतन्त्र चर हैं। [ V 1 I 2 ] = [ h 11 h 12 h 21 h 22 ] [ I 1 V 2 ] {\displaystyle \left[{\begin{array}{c}V_{1}\\I_{2}\end{array}}\right]=\left[{\begin{array}{cc}h_{11}&h_{12}\\h_{21}&h_{22}\end{array}}\right]\left[{\begin{array}{c}I_{1}\\V_{2}\end{array}}\right]} जहाँ
h 11 = V 1 I 1 | V 2 = 0 h 12 = V 1 V 2 | I 1 = 0 {\displaystyle h_{11}={V_{1} \over I_{1}}{\bigg |}_{V_{2}=0}\qquad h_{12}={V_{1} \over V_{2}}{\bigg |}_{I_{1}=0}} h 21 = I 2 I 1 | V 2 = 0 h 22 = I 2 V 2 | I 1 = 0 {\displaystyle h_{21}={I_{2} \over I_{1}}{\bigg |}_{V_{2}=0}\qquad h_{22}={I_{2} \over V_{2}}{\bigg |}_{I_{1}=0}} ध्यान दें कि h प्राचलों की विमाएँ अलग-अलग है। इसी लिए इन्हें संकर प्राचल कहते हैं। इसमें से जो प्राचल मुख्य तिर्यक रेखा पर नहीं हैं वे बिमारहित हैं (इनका कोई मात्रक नहीं है।)।
[ V 1 I 1 ] = [ A B C D ] [ V 2 − I 2 ] {\displaystyle {\begin{bmatrix}V_{1}\\I_{1}\end{bmatrix}}={\begin{bmatrix}A&B\\C&D\end{bmatrix}}{\begin{bmatrix}V_{2}\\-I_{2}\end{bmatrix}}} जहाँ
A = V 1 V 2 | I 2 = 0 B = − V 1 I 2 | V 2 = 0 {\displaystyle A={V_{1} \over V_{2}}{\bigg |}_{I_{2}=0}\qquad B=-{V_{1} \over I_{2}}{\bigg |}_{V_{2}=0}} C = I 1 V 2 | I 2 = 0 D = − I 1 I 2 | V 2 = 0 {\displaystyle C={I_{1} \over V_{2}}{\bigg |}_{I_{2}=0}\qquad D=-{I_{1} \over I_{2}}{\bigg |}_{V_{2}=0}} व्युत्क्रम नेटवर्क के लिए,A D − B C = 1 {\displaystyle \textstyle AD-BC=1} A = D {\displaystyle \textstyle A=D} A और D वास्तविक संख्याएँ होंगी जबकि B और C पूर्णतः काल्पनिक संख्याएँ ।
( I 1 V 2 ) = ( g 11 g 12 g 21 g 22 ) ( V 1 I 2 ) {\displaystyle {I_{1} \choose V_{2}}={\begin{pmatrix}g_{11}&g_{12}\\g_{21}&g_{22}\end{pmatrix}}{V_{1} \choose I_{2}}} जहाँ
g 11 = I 1 V 1 | I 2 = 0 g 12 = I 1 I 2 | V 1 = 0 {\displaystyle g_{11}={I_{1} \over V_{1}}{\bigg |}_{I_{2}=0}\qquad g_{12}={I_{1} \over I_{2}}{\bigg |}_{V_{1}=0}} g 21 = V 2 V 1 | I 2 = 0 g 22 = V 2 I 2 | V 1 = 0 {\displaystyle g_{21}={V_{2} \over V_{1}}{\bigg |}_{I_{2}=0}\qquad g_{22}={V_{2} \over I_{2}}{\bigg |}_{V_{1}=0}}
[ z ] {\displaystyle \mathbf {[z]} } [ y ] {\displaystyle \mathbf {[y]} } [ h ] {\displaystyle \mathbf {[h]} } [ g ] {\displaystyle \mathbf {[g]} } [ a ] {\displaystyle \mathbf {[a]} } [ b ] {\displaystyle \mathbf {[b]} } [ z ] {\displaystyle \mathbf {[z]} } [ z 11 z 12 z 21 z 22 ] {\displaystyle {\begin{bmatrix}z_{11}&z_{12}\\z_{21}&z_{22}\end{bmatrix}}} 1 Δ [ y ] [ y 22 − y 12 − y 21 y 11 ] {\displaystyle {\frac {1}{\Delta \mathbf {[y]} }}{\begin{bmatrix}y_{22}&-y_{12}\\-y_{21}&y_{11}\end{bmatrix}}} 1 h 22 [ Δ [ h ] h 12 − h 21 1 ] {\displaystyle {\frac {1}{h_{22}}}{\begin{bmatrix}\Delta \mathbf {[h]} &h_{12}\\-h_{21}&1\end{bmatrix}}} 1 g 11 [ 1 − g 12 g 21 Δ [ g ] ] {\displaystyle {\frac {1}{g_{11}}}{\begin{bmatrix}1&-g_{12}\\g_{21}&\Delta \mathbf {[g]} \end{bmatrix}}} 1 a 21 [ a 11 Δ [ a ] 1 a 22 ] {\displaystyle {\frac {1}{a_{21}}}{\begin{bmatrix}a_{11}&\Delta \mathbf {[a]} \\1&a_{22}\end{bmatrix}}} 1 b 21 [ − b 22 − 1 − Δ [ b ] − b 11 ] {\displaystyle {\frac {1}{b_{21}}}{\begin{bmatrix}-b_{22}&-1\\-\Delta \mathbf {[b]} &-b_{11}\end{bmatrix}}} [ y ] {\displaystyle \mathbf {[y]} } 1 Δ [ z ] [ z 22 − z 12 − z 21 z 11 ] {\displaystyle {\frac {1}{\Delta \mathbf {[z]} }}{\begin{bmatrix}z_{22}&-z_{12}\\-z_{21}&z_{11}\end{bmatrix}}} [ y 11 y 12 y 21 y 22 ] {\displaystyle {\begin{bmatrix}y_{11}&y_{12}\\y_{21}&y_{22}\end{bmatrix}}} 1 h 11 [ 1 − h 12 h 21 Δ [ h ] ] {\displaystyle {\frac {1}{h_{11}}}{\begin{bmatrix}1&-h_{12}\\h_{21}&\Delta \mathbf {[h]} \end{bmatrix}}} 1 g 22 [ Δ [ g ] g 12 − g 21 1 ] {\displaystyle {\frac {1}{g_{22}}}{\begin{bmatrix}\Delta \mathbf {[g]} &g_{12}\\-g_{21}&1\end{bmatrix}}} 1 a 12 [ a 22 − Δ [ a ] − 1 a 11 ] {\displaystyle {\frac {1}{a_{12}}}{\begin{bmatrix}a_{22}&-\Delta \mathbf {[a]} \\-1&a_{11}\end{bmatrix}}} 1 b 12 [ − b 11 1 Δ [ b ] − b 22 ] {\displaystyle {\frac {1}{b_{12}}}{\begin{bmatrix}-b_{11}&1\\\Delta \mathbf {[b]} &-b_{22}\end{bmatrix}}} [ h ] {\displaystyle \mathbf {[h]} } 1 z 22 [ Δ [ z ] z 12 − z 21 1 ] {\displaystyle {\frac {1}{z_{22}}}{\begin{bmatrix}\Delta \mathbf {[z]} &z_{12}\\-z_{21}&1\end{bmatrix}}} 1 y 11 [ 1 − y 12 y 21 Δ [ y ] ] {\displaystyle {\frac {1}{y_{11}}}{\begin{bmatrix}1&-y_{12}\\y_{21}&\Delta \mathbf {[y]} \end{bmatrix}}} [ h 11 h 12 h 21 h 22 ] {\displaystyle {\begin{bmatrix}h_{11}&h_{12}\\h_{21}&h_{22}\end{bmatrix}}} 1 Δ [ g ] [ g 22 − g 12 − g 21 g 11 ] {\displaystyle {\frac {1}{\Delta \mathbf {[g]} }}{\begin{bmatrix}g_{22}&-g_{12}\\-g_{21}&g_{11}\end{bmatrix}}} 1 a 22 [ a 12 Δ [ a ] − 1 a 21 ] {\displaystyle {\frac {1}{a_{22}}}{\begin{bmatrix}a_{12}&\Delta \mathbf {[a]} \\-1&a_{21}\end{bmatrix}}} 1 b 11 [ − b 12 1 − Δ [ b ] − b 21 ] {\displaystyle {\frac {1}{b_{11}}}{\begin{bmatrix}-b_{12}&1\\-\Delta \mathbf {[b]} &-b_{21}\end{bmatrix}}} [ g ] {\displaystyle \mathbf {[g]} } 1 z 11 [ 1 − z 12 z 21 Δ [ z ] ] {\displaystyle {\frac {1}{z_{11}}}{\begin{bmatrix}1&-z_{12}\\z_{21}&\Delta \mathbf {[z]} \end{bmatrix}}} 1 y 22 [ Δ [ y ] y 12 − y 21 1 ] {\displaystyle {\frac {1}{y_{22}}}{\begin{bmatrix}\Delta \mathbf {[y]} &y_{12}\\-y_{21}&1\end{bmatrix}}} 1 Δ [ h ] [ h 22 − h 12 − h 21 h 11 ] {\displaystyle {\frac {1}{\Delta \mathbf {[h]} }}{\begin{bmatrix}h_{22}&-h_{12}\\-h_{21}&h_{11}\end{bmatrix}}} [ g 11 g 12 g 21 g 22 ] {\displaystyle {\begin{bmatrix}g_{11}&g_{12}\\g_{21}&g_{22}\end{bmatrix}}} 1 a 11 [ a 21 − Δ [ a ] 1 a 12 ] {\displaystyle {\frac {1}{a_{11}}}{\begin{bmatrix}a_{21}&-\Delta \mathbf {[a]} \\1&a_{12}\end{bmatrix}}} 1 b 22 [ − b 21 − 1 Δ [ b ] − b 12 ] {\displaystyle {\frac {1}{b_{22}}}{\begin{bmatrix}-b_{21}&-1\\\Delta \mathbf {[b]} &-b_{12}\end{bmatrix}}} [ a ] {\displaystyle \mathbf {[a]} } 1 z 21 [ z 11 Δ [ z ] 1 z 22 ] {\displaystyle {\frac {1}{z_{21}}}{\begin{bmatrix}z_{11}&\Delta \mathbf {[z]} \\1&z_{22}\end{bmatrix}}} 1 y 21 [ − y 22 − 1 − Δ [ y ] − y 11 ] {\displaystyle {\frac {1}{y_{21}}}{\begin{bmatrix}-y_{22}&-1\\-\Delta \mathbf {[y]} &-y_{11}\end{bmatrix}}} 1 h 21 [ − Δ [ h ] − h 11 − h 22 − 1 ] {\displaystyle {\frac {1}{h_{21}}}{\begin{bmatrix}-\Delta \mathbf {[h]} &-h_{11}\\-h_{22}&-1\end{bmatrix}}} 1 g 21 [ 1 g 22 g 11 Δ [ g ] ] {\displaystyle {\frac {1}{g_{21}}}{\begin{bmatrix}1&g_{22}\\g_{11}&\Delta \mathbf {[g]} \end{bmatrix}}} [ a 11 a 12 a 21 a 22 ] {\displaystyle {\begin{bmatrix}a_{11}&a_{12}\\a_{21}&a_{22}\end{bmatrix}}} 1 Δ [ b ] [ b 22 − b 12 − b 21 b 11 ] {\displaystyle {\frac {1}{\Delta \mathbf {[b]} }}{\begin{bmatrix}b_{22}&-b_{12}\\-b_{21}&b_{11}\end{bmatrix}}} [ b ] {\displaystyle \mathbf {[b]} } 1 z 12 [ z 22 − Δ [ z ] − 1 z 11 ] {\displaystyle {\frac {1}{z_{12}}}{\begin{bmatrix}z_{22}&-\Delta \mathbf {[z]} \\-1&z_{11}\end{bmatrix}}} 1 y 12 [ − y 11 1 Δ [ y ] − y 22 ] {\displaystyle {\frac {1}{y_{12}}}{\begin{bmatrix}-y_{11}&1\\\Delta \mathbf {[y]} &-y_{22}\end{bmatrix}}} 1 h 12 [ 1 − h 11 − h 22 Δ [ h ] ] {\displaystyle {\frac {1}{h_{12}}}{\begin{bmatrix}1&-h_{11}\\-h_{22}&\Delta \mathbf {[h]} \end{bmatrix}}} 1 g 12 [ − Δ [ g ] g 22 g 11 − 1 ] {\displaystyle {\frac {1}{g_{12}}}{\begin{bmatrix}-\Delta \mathbf {[g]} &g_{22}\\g_{11}&-1\end{bmatrix}}} 1 Δ [ a ] [ a 22 − a 12 − a 21 a 11 ] {\displaystyle {\frac {1}{\Delta \mathbf {[a]} }}{\begin{bmatrix}a_{22}&-a_{12}\\-a_{21}&a_{11}\end{bmatrix}}} [ b 11 b 12 b 21 b 22 ] {\displaystyle {\begin{bmatrix}b_{11}&b_{12}\\b_{21}&b_{22}\end{bmatrix}}}
जहाँ Δ [ x ] {\displaystyle \Delta \mathbf {[x]} } x ] का सारणिक है।
कुछ मैट्रिक्स जोड़ों में बहुत सरल सम्बन्ध है। ऐडमिटैन्स पैरामीट्र्स, इम्पीडैन्स पैरामीट्र्स के मैट्रिक्स व्युत्क्रम हैं। इन्वर्स हाइब्रिड पैरामीटर्स, हाइब्रिड पैरामीट्र्स के मैट्रिक्स व्युत्क्रम हैं। इसी प्रकार ABCD-पैरामीटर्स का [b ] स्वरूप, [a ] स्वरूप का मैट्रिक्स व्युक्रम है। अर्थात्,
[ y ] = [ z ] − 1 [ g ] = [ h ] − 1 [ b ] = [ a ] − 1 {\displaystyle {\begin{aligned}\left[\mathbf {y} \right]&=\left[\mathbf {z} \right]^{-1}\\\left[\mathbf {g} \right]&=\left[\mathbf {h} \right]^{-1}\\\left[\mathbf {b} \right]&=\left[\mathbf {a} \right]^{-1}\end{aligned}}} 


![{\displaystyle \left[{\begin{array}{c}V_{1}\\V_{2}\end{array}}\right]=\left[{\begin{array}{cc}z_{11}&z_{12}\\z_{21}&z_{22}\end{array}}\right]\left[{\begin{array}{c}I_{1}\\I_{2}\end{array}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7645f82f97b057892f6d77d80bbf01b985aaae0f)


![{\displaystyle \left[{\begin{array}{c}I_{1}\\I_{2}\end{array}}\right]=\left[{\begin{array}{cc}y_{11}&y_{12}\\y_{21}&y_{22}\end{array}}\right]\left[{\begin{array}{c}V_{1}\\V_{2}\end{array}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1f0a34623af2771a0510c92e6a21ac4e6de760aa)



![{\displaystyle \left[{\begin{array}{c}V_{1}\\I_{2}\end{array}}\right]=\left[{\begin{array}{cc}h_{11}&h_{12}\\h_{21}&h_{22}\end{array}}\right]\left[{\begin{array}{c}I_{1}\\V_{2}\end{array}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1c00cbb49d25bac33d7604001e899611b35d1cb1)


































![{\displaystyle \mathbf {[z]} }](https://wikimedia.org/api/rest_v1/media/math/render/svg/39a15629f53e59d8b3f33c46e53f611263cfd316)
![{\displaystyle \mathbf {[y]} }](https://wikimedia.org/api/rest_v1/media/math/render/svg/d4458b2ca484d04257ccef4cb8c8d69f741259a1)
![{\displaystyle \mathbf {[h]} }](https://wikimedia.org/api/rest_v1/media/math/render/svg/909c87cfcffae56fc82c9a9a1a64acf567c95d0d)
![{\displaystyle \mathbf {[g]} }](https://wikimedia.org/api/rest_v1/media/math/render/svg/dd1bb163d1cf09415eeb03f281e9da0198a7c62c)
![{\displaystyle \mathbf {[a]} }](https://wikimedia.org/api/rest_v1/media/math/render/svg/b131c25f3dd29ad2f346fd38eef0e0f82141a17c)
![{\displaystyle \mathbf {[b]} }](https://wikimedia.org/api/rest_v1/media/math/render/svg/14a7b4c3024361dc694ccc9bc7c8a59455c6af22)

![{\displaystyle {\frac {1}{\Delta \mathbf {[y]} }}{\begin{bmatrix}y_{22}&-y_{12}\\-y_{21}&y_{11}\end{bmatrix}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1c88ffe2d04c66ea158cce57f580cd5267abce0e)
![{\displaystyle {\frac {1}{h_{22}}}{\begin{bmatrix}\Delta \mathbf {[h]} &h_{12}\\-h_{21}&1\end{bmatrix}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/679350eeb4501fdcbb765109982cba5ee87702cb)
![{\displaystyle {\frac {1}{g_{11}}}{\begin{bmatrix}1&-g_{12}\\g_{21}&\Delta \mathbf {[g]} \end{bmatrix}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7571ffabfe73601c1f386526f47f7cb93df0dc21)
![{\displaystyle {\frac {1}{a_{21}}}{\begin{bmatrix}a_{11}&\Delta \mathbf {[a]} \\1&a_{22}\end{bmatrix}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c2854821de24f97e711f6663b0b4b90f5365fcb1)
![{\displaystyle {\frac {1}{b_{21}}}{\begin{bmatrix}-b_{22}&-1\\-\Delta \mathbf {[b]} &-b_{11}\end{bmatrix}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b42b94e8f71b186b145ef74378c440bb77ac2387)
![{\displaystyle {\frac {1}{\Delta \mathbf {[z]} }}{\begin{bmatrix}z_{22}&-z_{12}\\-z_{21}&z_{11}\end{bmatrix}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/487dab825b656f1e0a2d73e74172948e52da3a91)

![{\displaystyle {\frac {1}{h_{11}}}{\begin{bmatrix}1&-h_{12}\\h_{21}&\Delta \mathbf {[h]} \end{bmatrix}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/04bd8b306b3b259f0137fa39e0d23636bf9dd095)
![{\displaystyle {\frac {1}{g_{22}}}{\begin{bmatrix}\Delta \mathbf {[g]} &g_{12}\\-g_{21}&1\end{bmatrix}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1f1754d13c9fd54602ce8548754165b669811e3d)
![{\displaystyle {\frac {1}{a_{12}}}{\begin{bmatrix}a_{22}&-\Delta \mathbf {[a]} \\-1&a_{11}\end{bmatrix}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c802d740f72fc6175de957e2cf1ee95f3cbc4c93)
![{\displaystyle {\frac {1}{b_{12}}}{\begin{bmatrix}-b_{11}&1\\\Delta \mathbf {[b]} &-b_{22}\end{bmatrix}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/dbb283ff7b662b2be5dee2ed4b60a5cf06c8a949)
![{\displaystyle {\frac {1}{z_{22}}}{\begin{bmatrix}\Delta \mathbf {[z]} &z_{12}\\-z_{21}&1\end{bmatrix}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a3547f1e5ce30efd98cfadc48955972100ef1fb7)
![{\displaystyle {\frac {1}{y_{11}}}{\begin{bmatrix}1&-y_{12}\\y_{21}&\Delta \mathbf {[y]} \end{bmatrix}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e108f5071a85ed3923a1eee1f1b01280651019e8)

![{\displaystyle {\frac {1}{\Delta \mathbf {[g]} }}{\begin{bmatrix}g_{22}&-g_{12}\\-g_{21}&g_{11}\end{bmatrix}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8460f7065162ca83b30f80322090b39409a2f993)
![{\displaystyle {\frac {1}{a_{22}}}{\begin{bmatrix}a_{12}&\Delta \mathbf {[a]} \\-1&a_{21}\end{bmatrix}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/73f2d30b43344b899a3d580c9839d711bcfaa088)
![{\displaystyle {\frac {1}{b_{11}}}{\begin{bmatrix}-b_{12}&1\\-\Delta \mathbf {[b]} &-b_{21}\end{bmatrix}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/26b3d40e5e3b4804b2bf4ae9bb4d7a6a3466a9ec)
![{\displaystyle {\frac {1}{z_{11}}}{\begin{bmatrix}1&-z_{12}\\z_{21}&\Delta \mathbf {[z]} \end{bmatrix}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/632efee553a0074f0a53f3728daabc61efc228e2)
![{\displaystyle {\frac {1}{y_{22}}}{\begin{bmatrix}\Delta \mathbf {[y]} &y_{12}\\-y_{21}&1\end{bmatrix}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/07b0048de9c42457c78987ff24cdbb163413041f)
![{\displaystyle {\frac {1}{\Delta \mathbf {[h]} }}{\begin{bmatrix}h_{22}&-h_{12}\\-h_{21}&h_{11}\end{bmatrix}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/732cd41db04bcb0d04be3afe420d93bf926501f5)

![{\displaystyle {\frac {1}{a_{11}}}{\begin{bmatrix}a_{21}&-\Delta \mathbf {[a]} \\1&a_{12}\end{bmatrix}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/cbc02229992524f2d4b9b2ff429081aa8c3259dd)
![{\displaystyle {\frac {1}{b_{22}}}{\begin{bmatrix}-b_{21}&-1\\\Delta \mathbf {[b]} &-b_{12}\end{bmatrix}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/65e27a58d182069a1604adea4d34a0414c235965)
![{\displaystyle {\frac {1}{z_{21}}}{\begin{bmatrix}z_{11}&\Delta \mathbf {[z]} \\1&z_{22}\end{bmatrix}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e9e1df73c8bd4dff60b2bc2eadc0abb52eead96d)
![{\displaystyle {\frac {1}{y_{21}}}{\begin{bmatrix}-y_{22}&-1\\-\Delta \mathbf {[y]} &-y_{11}\end{bmatrix}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/68c776cac7d0c011700f7ce937cffd37455c38d4)
![{\displaystyle {\frac {1}{h_{21}}}{\begin{bmatrix}-\Delta \mathbf {[h]} &-h_{11}\\-h_{22}&-1\end{bmatrix}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ea019358559b8ba1b9ae3abb899e3db9e1875475)
![{\displaystyle {\frac {1}{g_{21}}}{\begin{bmatrix}1&g_{22}\\g_{11}&\Delta \mathbf {[g]} \end{bmatrix}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/269fc51350d7ded4803b758f27ff12cb80e73beb)

![{\displaystyle {\frac {1}{\Delta \mathbf {[b]} }}{\begin{bmatrix}b_{22}&-b_{12}\\-b_{21}&b_{11}\end{bmatrix}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/86ca4b289ed3c07c833c3001ee10168d417a42ab)
![{\displaystyle {\frac {1}{z_{12}}}{\begin{bmatrix}z_{22}&-\Delta \mathbf {[z]} \\-1&z_{11}\end{bmatrix}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8c40fe17c9e9399ea4ada9238208b9d8e7a99098)
![{\displaystyle {\frac {1}{y_{12}}}{\begin{bmatrix}-y_{11}&1\\\Delta \mathbf {[y]} &-y_{22}\end{bmatrix}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/33262946d25e353d1f51cc00e9372c153b105fbd)
![{\displaystyle {\frac {1}{h_{12}}}{\begin{bmatrix}1&-h_{11}\\-h_{22}&\Delta \mathbf {[h]} \end{bmatrix}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/69984c19e2082dea86e684591755600b7d2d43de)
![{\displaystyle {\frac {1}{g_{12}}}{\begin{bmatrix}-\Delta \mathbf {[g]} &g_{22}\\g_{11}&-1\end{bmatrix}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5cc585f3a56517316e99dafcf64df6d476b2618a)
![{\displaystyle {\frac {1}{\Delta \mathbf {[a]} }}{\begin{bmatrix}a_{22}&-a_{12}\\-a_{21}&a_{11}\end{bmatrix}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/122338c08414e1803e057a4a3d235287d6492234)

![{\displaystyle \Delta \mathbf {[x]} }](https://wikimedia.org/api/rest_v1/media/math/render/svg/ec96dac6570532c10d6a07cafd3bf20df6722821)
![{\displaystyle {\begin{aligned}\left[\mathbf {y} \right]&=\left[\mathbf {z} \right]^{-1}\\\left[\mathbf {g} \right]&=\left[\mathbf {h} \right]^{-1}\\\left[\mathbf {b} \right]&=\left[\mathbf {a} \right]^{-1}\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a4da88c5d11c5e62d3817aad8c1299c8f5cccba5)