इस लेख में प्रमुख त्रिकोणमितीय सर्वसमिकाओं की उपपतियां (सिद्धि) दी गयीं हैं।
Trigonometric functions specify the relationships between side lengths and interior angles of a right triangle. For example, the sine of angle θ is defined as being the length of the opposite side divided by the length of the hypotenuse. Referring to the diagram at the right, the six trigonometric functions of θ are:
sin θ = o p p o s i t e h y p o t e n u s e = a h {\displaystyle \sin \theta ={\frac {\mathrm {opposite} }{\mathrm {hypotenuse} }}={\frac {a}{h}}} cos θ = a d j a c e n t h y p o t e n u s e = b h {\displaystyle \cos \theta ={\frac {\mathrm {adjacent} }{\mathrm {hypotenuse} }}={\frac {b}{h}}} tan θ = o p p o s i t e a d j a c e n t = a b {\displaystyle \tan \theta ={\frac {\mathrm {opposite} }{\mathrm {adjacent} }}={\frac {a}{b}}} cot θ = a d j a c e n t o p p o s i t e = b a {\displaystyle \cot \theta ={\frac {\mathrm {adjacent} }{\mathrm {opposite} }}={\frac {b}{a}}} sec θ = h y p o t e n u s e a d j a c e n t = h b {\displaystyle \sec \theta ={\frac {\mathrm {hypotenuse} }{\mathrm {adjacent} }}={\frac {h}{b}}} csc θ = h y p o t e n u s e o p p o s i t e = h a {\displaystyle \csc \theta ={\frac {\mathrm {hypotenuse} }{\mathrm {opposite} }}={\frac {h}{a}}}
The following identities are trivial algebraic consequences of these definitions and the division identity.
a b = ( a c ) ( b c ) {\displaystyle {\frac {a}{b}}={\frac {\left({\frac {a}{c}}\right)}{\left({\frac {b}{c}}\right)}}} tan θ = o p p o s i t e a d j a c e n t = ( o p p o s i t e h y p o t e n u s e ) ( a d j a c e n t h y p o t e n u s e ) = sin θ cos θ {\displaystyle \tan \theta ={\frac {\mathrm {opposite} }{\mathrm {adjacent} }}={\frac {\left({\frac {\mathrm {opposite} }{\mathrm {hypotenuse} }}\right)}{\left({\frac {\mathrm {adjacent} }{\mathrm {hypotenuse} }}\right)}}={\frac {\sin \theta }{\cos \theta }}} cot θ = a d j a c e n t o p p o s i t e = ( a d j a c e n t a d j a c e n t ) ( o p p o s i t e a d j a c e n t ) = 1 tan θ = cos θ sin θ {\displaystyle \cot \theta ={\frac {\mathrm {adjacent} }{\mathrm {opposite} }}={\frac {\left({\frac {\mathrm {adjacent} }{\mathrm {adjacent} }}\right)}{\left({\frac {\mathrm {opposite} }{\mathrm {adjacent} }}\right)}}={\frac {1}{\tan \theta }}={\frac {\cos \theta }{\sin \theta }}} sec θ = 1 cos θ = h y p o t e n u s e a d j a c e n t {\displaystyle \sec \theta ={\frac {1}{\cos \theta }}={\frac {\mathrm {hypotenuse} }{\mathrm {adjacent} }}} csc θ = 1 sin θ = h y p o t e n u s e o p p o s i t e {\displaystyle \csc \theta ={\frac {1}{\sin \theta }}={\frac {\mathrm {hypotenuse} }{\mathrm {opposite} }}} tan θ = o p p o s i t e a d j a c e n t = ( o p p o s i t e × h y p o t e n u s e o p p o s i t e × a d j a c e n t ) ( a d j a c e n t × h y p o t e n u s e o p p o s i t e × a d j a c e n t ) = ( h y p o t e n u s e a d j a c e n t ) ( h y p o t e n u s e o p p o s i t e ) = sec θ csc θ {\displaystyle \tan \theta ={\frac {\mathrm {opposite} }{\mathrm {adjacent} }}={\frac {\left({\frac {\mathrm {opposite} \times \mathrm {hypotenuse} }{\mathrm {opposite} \times \mathrm {adjacent} }}\right)}{\left({\frac {\mathrm {adjacent} \times \mathrm {hypotenuse} }{\mathrm {opposite} \times \mathrm {adjacent} }}\right)}}={\frac {\left({\frac {\mathrm {hypotenuse} }{\mathrm {adjacent} }}\right)}{\left({\frac {\mathrm {hypotenuse} }{\mathrm {opposite} }}\right)}}={\frac {\sec \theta }{\csc \theta }}} Or
tan θ = sin θ cos θ = ( 1 csc θ ) ( 1 sec θ ) = ( csc θ sec θ csc θ ) ( csc θ sec θ sec θ ) = sec θ csc θ {\displaystyle \tan \theta ={\frac {\sin \theta }{\cos \theta }}={\frac {\left({\frac {1}{\csc \theta }}\right)}{\left({\frac {1}{\sec \theta }}\right)}}={\frac {\left({\frac {\csc \theta \sec \theta }{\csc \theta }}\right)}{\left({\frac {\csc \theta \sec \theta }{\sec \theta }}\right)}}={\frac {\sec \theta }{\csc \theta }}} cot θ = csc θ sec θ {\displaystyle \cot \theta ={\frac {\csc \theta }{\sec \theta }}}
Two angles whose sum is π/2 radians (90 degrees) are complementary . In the diagram, the angles at vertices A and B are complementary, so we can exchange a and b, and change θ to π/2 − θ, obtaining:
sin ( π / 2 − θ ) = cos θ {\displaystyle \sin \left(\pi /2-\theta \right)=\cos \theta } cos ( π / 2 − θ ) = sin θ {\displaystyle \cos \left(\pi /2-\theta \right)=\sin \theta } tan ( π / 2 − θ ) = cot θ {\displaystyle \tan \left(\pi /2-\theta \right)=\cot \theta } cot ( π / 2 − θ ) = tan θ {\displaystyle \cot \left(\pi /2-\theta \right)=\tan \theta } sec ( π / 2 − θ ) = sec θ {\displaystyle \sec \left(\pi /2-\theta \right)=\sec \theta } csc ( π / 2 − θ ) = csc θ {\displaystyle \csc \left(\pi /2-\theta \right)=\csc \theta }
Identity 1:
sin 2 ( x ) + cos 2 ( x ) = 1 {\displaystyle \sin ^{2}(x)+\cos ^{2}(x)=1\,} Proof 1:
Refer to the triangle diagram above. Note that a 2 + b 2 = h 2 {\displaystyle a^{2}+b^{2}=h^{2}} Pythagorean theorem .
sin 2 ( x ) + cos 2 ( x ) = a 2 h 2 + b 2 h 2 = a 2 + b 2 h 2 = h 2 h 2 = 1. {\displaystyle \sin ^{2}(x)+\cos ^{2}(x)={\frac {a^{2}}{h^{2}}}+{\frac {b^{2}}{h^{2}}}={\frac {a^{2}+b^{2}}{h^{2}}}={\frac {h^{2}}{h^{2}}}=1.\,} The following two results follow from this and the ratio identities. To obtain the first, divide both sides of sin 2 ( x ) + cos 2 ( x ) = 1 {\displaystyle \sin ^{2}(x)+\cos ^{2}(x)=1} cos 2 ( x ) {\displaystyle \cos ^{2}(x)} sin 2 ( x ) {\displaystyle \sin ^{2}(x)}
tan 2 ( x ) + 1 = sec 2 ( x ) {\displaystyle \tan ^{2}(x)+1\ =\sec ^{2}(x)} sec 2 ( x ) − tan 2 ( x ) = 1 {\displaystyle \sec ^{2}(x)-\tan ^{2}(x)=1\ } Similarly
1 + cot 2 ( x ) = csc 2 ( x ) {\displaystyle 1\ +\cot ^{2}(x)=\csc ^{2}(x)} csc 2 ( x ) − cot 2 ( x ) = 1 {\displaystyle \csc ^{2}(x)-\cot ^{2}(x)=1\ } Proof 2:
Differentiating the left-hand side of the identity yields:
2 sin x ⋅ cos x − 2 sin x ⋅ cos x = 0 {\displaystyle 2\sin x\cdot \cos x-2\sin x\cdot \cos x=0} Integrating this shows that the original identity is equal to a constant, and this constant can be found by plugging in any arbitrary value of x.
Identity 2:
The following accounts for all three reciprocal functions.
csc 2 ( x ) + sec 2 ( x ) − cot 2 ( x ) = 2 + tan 2 ( x ) {\displaystyle \csc ^{2}(x)+\sec ^{2}(x)-\cot ^{2}(x)=2\ +\tan ^{2}(x)} Proof 1:
Refer to the triangle diagram above. Note that a 2 + b 2 = h 2 {\displaystyle a^{2}+b^{2}=h^{2}} Pythagorean theorem .
csc 2 ( x ) + sec 2 ( x ) = h 2 a 2 + h 2 b 2 = a 2 + b 2 a 2 + a 2 + b 2 b 2 = 2 + b 2 a 2 + a 2 b 2 {\displaystyle \csc ^{2}(x)+\sec ^{2}(x)={\frac {h^{2}}{a^{2}}}+{\frac {h^{2}}{b^{2}}}={\frac {a^{2}+b^{2}}{a^{2}}}+{\frac {a^{2}+b^{2}}{b^{2}}}=2\ +{\frac {b^{2}}{a^{2}}}+{\frac {a^{2}}{b^{2}}}} Substituting with appropriate functions -
2 + b 2 a 2 + a 2 b 2 = 2 + tan 2 ( x ) + cot 2 ( x ) {\displaystyle 2\ +{\frac {b^{2}}{a^{2}}}+{\frac {a^{2}}{b^{2}}}=2\ +\tan ^{2}(x)+\cot ^{2}(x)} Rearranging gives:
csc 2 ( x ) + sec 2 ( x ) − cot 2 ( x ) = 2 + tan 2 ( x ) {\displaystyle \csc ^{2}(x)+\sec ^{2}(x)-\cot ^{2}(x)=2\ +\tan ^{2}(x)}
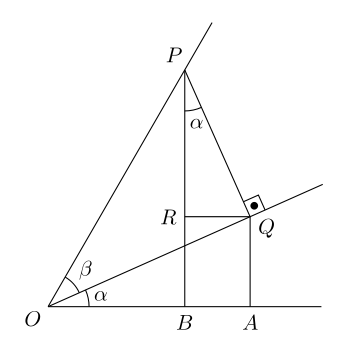
Illustration of the sum formula. Draw a horizontal line (the x -axis); mark an origin O. Draw a line from O at an angle α {\displaystyle \alpha } β {\displaystyle \beta } x -axis is α + β {\displaystyle \alpha +\beta }
Place P on the line defined by α + β {\displaystyle \alpha +\beta }
Let PQ be a line perpendicular to line defined by angle α {\displaystyle \alpha } ∴ {\displaystyle \therefore }
Let QA be a perpendicular from point A on the x -axis to Q and PB be a perpendicular from point B on the x -axis to P. ∴ {\displaystyle \therefore }
Draw QR parallel to the x -axis.
Now angle R P Q = α {\displaystyle RPQ=\alpha } O Q A = 90 − α {\displaystyle OQA=90-\alpha } R Q O = α , R Q P = 90 − α {\displaystyle RQO=\alpha ,RQP=90-\alpha } R P Q = α {\displaystyle RPQ=\alpha }
R P Q = π 2 − R Q P = π 2 − ( π 2 − R Q O ) = R Q O = α {\displaystyle RPQ={\tfrac {\pi }{2}}-RQP={\tfrac {\pi }{2}}-({\tfrac {\pi }{2}}-RQO)=RQO=\alpha } O P = 1 {\displaystyle OP=1} P Q = sin β {\displaystyle PQ=\sin \beta } O Q = cos β {\displaystyle OQ=\cos \beta } A Q O Q = sin α {\displaystyle {\frac {AQ}{OQ}}=\sin \alpha \,} A Q = sin α cos β {\displaystyle AQ=\sin \alpha \cos \beta } P R P Q = cos α {\displaystyle {\frac {PR}{PQ}}=\cos \alpha \,} P R = cos α sin β {\displaystyle PR=\cos \alpha \sin \beta } sin ( α + β ) = P B = R B + P R = A Q + P R = sin α cos β + cos α sin β {\displaystyle \sin(\alpha +\beta )=PB=RB+PR=AQ+PR=\sin \alpha \cos \beta +\cos \alpha \sin \beta } By substituting − β {\displaystyle -\beta } β {\displaystyle \beta } Symmetry , we also get:
sin ( α − β ) = sin α cos − β + cos α sin − β {\displaystyle \sin(\alpha -\beta )=\sin \alpha \cos -\beta +\cos \alpha \sin -\beta } sin ( α − β ) = sin α cos β − cos α sin β {\displaystyle \sin(\alpha -\beta )=\sin \alpha \cos \beta -\cos \alpha \sin \beta } Another simple "proof" can be given using Euler's formula known from complex analysis: Euler's formula is:
e i φ = cos φ + i sin φ {\displaystyle e^{i\varphi }=\cos \varphi +i\sin \varphi } Although it is more precise to say that Euler's formula entails the trigonometric identities, it follows that for angles α {\displaystyle \alpha } β {\displaystyle \beta }
e i ( α + β ) = cos ( α + β ) + i sin ( α + β ) {\displaystyle e^{i(\alpha +\beta )}=\cos(\alpha +\beta )+i\sin(\alpha +\beta )} Also using the following properties of exponential functions:
e i ( α + β ) = e i α e i β = ( cos α + i sin α ) ( cos β + i sin β ) {\displaystyle e^{i(\alpha +\beta )}=e^{i\alpha }e^{i\beta }=(\cos \alpha +i\sin \alpha )(\cos \beta +i\sin \beta )} Evaluating the product:
e i ( α + β ) = ( cos α cos β − sin α sin β ) + i ( sin α cos β + sin β cos α ) {\displaystyle e^{i(\alpha +\beta )}=(\cos \alpha \cos \beta -\sin \alpha \sin \beta )+i(\sin \alpha \cos \beta +\sin \beta \cos \alpha )} Equating real and imaginary parts:
cos ( α + β ) = cos α cos β − sin α sin β {\displaystyle \cos(\alpha +\beta )=\cos \alpha \cos \beta -\sin \alpha \sin \beta } sin ( α + β ) = sin α cos β + sin β cos α {\displaystyle \sin(\alpha +\beta )=\sin \alpha \cos \beta +\sin \beta \cos \alpha }
Using the figure above,
O P = 1 {\displaystyle OP=1\,} P Q = sin β {\displaystyle PQ=\sin \beta \,} O Q = cos β {\displaystyle OQ=\cos \beta \,} O A O Q = cos α {\displaystyle {\frac {OA}{OQ}}=\cos \alpha \,} O A = cos α cos β {\displaystyle OA=\cos \alpha \cos \beta \,} R Q P Q = sin α {\displaystyle {\frac {RQ}{PQ}}=\sin \alpha \,} R Q = sin α sin β {\displaystyle RQ=\sin \alpha \sin \beta \,} cos ( α + β ) = O B = O A − B A = O A − R Q = cos α cos β − sin α sin β {\displaystyle \cos(\alpha +\beta )=OB=OA-BA=OA-RQ=\cos \alpha \cos \beta \ -\sin \alpha \sin \beta \,} By substituting − β {\displaystyle -\beta } β {\displaystyle \beta } Symmetry , we also get:
cos ( α − β ) = cos α cos − β − sin α sin − β {\displaystyle \cos(\alpha -\beta )=\cos \alpha \cos -\beta \ -\sin \alpha \sin -\beta \,} cos ( α − β ) = cos α cos β + sin α sin β {\displaystyle \cos(\alpha -\beta )=\cos \alpha \cos \beta +\sin \alpha \sin \beta \,} Also, using the complementary angle formulae,
cos ( α + β ) = sin ( π / 2 − ( α + β ) ) = sin ( ( π / 2 − α ) − β ) = sin ( π / 2 − α ) cos β − cos ( π / 2 − α ) sin β = cos α cos β − sin α sin β {\displaystyle {\begin{aligned}\cos(\alpha +\beta )&=\sin \left(\pi /2-(\alpha +\beta )\right)\\&=\sin \left((\pi /2-\alpha )-\beta \right)\\&=\sin \left(\pi /2-\alpha \right)\cos \beta -\cos \left(\pi /2-\alpha \right)\sin \beta \\&=\cos \alpha \cos \beta -\sin \alpha \sin \beta \\\end{aligned}}}
From the sine and cosine formulae, we get
tan ( α + β ) = sin ( α + β ) cos ( α + β ) = sin α cos β + cos α sin β cos α cos β − sin α sin β {\displaystyle \tan(\alpha +\beta )={\frac {\sin(\alpha +\beta )}{\cos(\alpha +\beta )}}={\frac {\sin \alpha \cos \beta +\cos \alpha \sin \beta }{\cos \alpha \cos \beta -\sin \alpha \sin \beta }}} Dividing both numerator and denominator by cos α cos β {\displaystyle \cos \alpha \cos \beta }
tan ( α + β ) = tan α + tan β 1 − tan α tan β {\displaystyle \tan(\alpha +\beta )={\frac {\tan \alpha +\tan \beta }{1-\tan \alpha \tan \beta }}} Subtracting β {\displaystyle \beta } α {\displaystyle \alpha } tan ( − β ) = − tan β {\displaystyle \tan(-\beta )=-\tan \beta }
tan ( α − β ) = tan α + tan ( − β ) 1 − tan α tan ( − β ) = tan α − tan β 1 + tan α tan β {\displaystyle \tan(\alpha -\beta )={\frac {\tan \alpha +\tan(-\beta )}{1-\tan \alpha \tan(-\beta )}}={\frac {\tan \alpha -\tan \beta }{1+\tan \alpha \tan \beta }}} Similarly from the sine and cosine formulae, we get
cot ( α + β ) = cos ( α + β ) sin ( α + β ) = cos α cos β − sin α sin β sin α cos β + cos α sin β {\displaystyle \cot(\alpha +\beta )={\frac {\cos(\alpha +\beta )}{\sin(\alpha +\beta )}}={\frac {\cos \alpha \cos \beta -\sin \alpha \sin \beta }{\sin \alpha \cos \beta +\cos \alpha \sin \beta }}} Then by dividing both numerator and denominator by sin α sin β {\displaystyle \sin \alpha \sin \beta }
cot ( α + β ) = cot α cot β − 1 cot α + cot β {\displaystyle \cot(\alpha +\beta )={\frac {\cot \alpha \cot \beta -1}{\cot \alpha +\cot \beta }}} Or, using cot θ = 1 tan θ {\displaystyle \cot \theta ={\frac {1}{\tan \theta }}}
cot ( α + β ) = 1 − tan α tan β tan α + tan β = 1 tan α tan β − 1 1 tan α + 1 tan β = cot α cot β − 1 cot α + cot β {\displaystyle \cot(\alpha +\beta )={\frac {1-\tan \alpha \tan \beta }{\tan \alpha +\tan \beta }}={\frac {{\frac {1}{\tan \alpha \tan \beta }}-1}{{\frac {1}{\tan \alpha }}+{\frac {1}{\tan \beta }}}}={\frac {\cot \alpha \cot \beta -1}{\cot \alpha +\cot \beta }}} Using cot ( − β ) = − cot β {\displaystyle \cot(-\beta )=-\cot \beta }
cot ( α − β ) = cot α cot ( − β ) − 1 cot α + cot ( − β ) = cot α cot β + 1 cot β − cot α {\displaystyle \cot(\alpha -\beta )={\frac {\cot \alpha \cot(-\beta )-1}{\cot \alpha +\cot(-\beta )}}={\frac {\cot \alpha \cot \beta +1}{\cot \beta -\cot \alpha }}}
From the angle sum identities, we get
sin ( 2 θ ) = 2 sin θ cos θ {\displaystyle \sin(2\theta )=2\sin \theta \cos \theta \,} and
cos ( 2 θ ) = cos 2 θ − sin 2 θ {\displaystyle \cos(2\theta )=\cos ^{2}\theta -\sin ^{2}\theta \,} The Pythagorean identities give the two alternative forms for the latter of these:
cos ( 2 θ ) = 2 cos 2 θ − 1 {\displaystyle \cos(2\theta )=2\cos ^{2}\theta -1\,} cos ( 2 θ ) = 1 − 2 sin 2 θ {\displaystyle \cos(2\theta )=1-2\sin ^{2}\theta \,} The angle sum identities also give
tan ( 2 θ ) = 2 tan θ 1 − tan 2 θ = 2 cot θ − tan θ {\displaystyle \tan(2\theta )={\frac {2\tan \theta }{1-\tan ^{2}\theta }}={\frac {2}{\cot \theta -\tan \theta }}\,} cot ( 2 θ ) = cot 2 θ − 1 2 cot θ = cot θ − tan θ 2 {\displaystyle \cot(2\theta )={\frac {\cot ^{2}\theta -1}{2\cot \theta }}={\frac {\cot \theta -\tan \theta }{2}}\,} It can also be proved using Euler's formula
e i φ = cos φ + i sin φ {\displaystyle e^{i\varphi }=\cos \varphi +i\sin \varphi } Squaring both sides yields
e i 2 φ = ( cos φ + i sin φ ) 2 {\displaystyle e^{i2\varphi }=(\cos \varphi +i\sin \varphi )^{2}} But replacing the angle with its doubled version, which achieves the same result in the left side of the equation, yields
e i 2 φ = cos 2 φ + i sin 2 φ {\displaystyle e^{i2\varphi }=\cos 2\varphi +i\sin 2\varphi } It follows that
( cos φ + i sin φ ) 2 = cos 2 φ + i sin 2 φ {\displaystyle (\cos \varphi +i\sin \varphi )^{2}=\cos 2\varphi +i\sin 2\varphi } Expanding the square and simplifying on the left hand side of the equation gives
i ( 2 sin φ cos φ ) + cos 2 φ − sin 2 φ = cos 2 φ + i sin 2 φ {\displaystyle i(2\sin \varphi \cos \varphi )+\cos ^{2}\varphi -\sin ^{2}\varphi \ =\cos 2\varphi +i\sin 2\varphi } Because the imaginary and real parts have to be the same, we are left with the original identities
cos 2 φ − sin 2 φ = cos 2 φ {\displaystyle \cos ^{2}\varphi -\sin ^{2}\varphi \ =\cos 2\varphi } and also
2 sin φ cos φ = sin 2 φ {\displaystyle 2\sin \varphi \cos \varphi =\sin 2\varphi }
The two identities giving the alternative forms for cos 2θ lead to the following equations:
cos θ 2 = ± 1 + cos θ 2 , {\displaystyle \cos {\frac {\theta }{2}}=\pm \,{\sqrt {\frac {1+\cos \theta }{2}}},\,} sin θ 2 = ± 1 − cos θ 2 . {\displaystyle \sin {\frac {\theta }{2}}=\pm \,{\sqrt {\frac {1-\cos \theta }{2}}}.\,} The sign of the square root needs to be chosen properly—note that if π is added to θ, the quantities inside the square roots are unchanged, but the left-hand-sides of the equations change sign. Therefore the correct sign to use depends on the value of θ.
For the tan function, the equation is:
tan θ 2 = ± 1 − cos θ 1 + cos θ . {\displaystyle \tan {\frac {\theta }{2}}=\pm \,{\sqrt {\frac {1-\cos \theta }{1+\cos \theta }}}.\,} Then multiplying the numerator and denominator inside the square root by (1 + cos θ) and using Pythagorean identities leads to:
tan θ 2 = sin θ 1 + cos θ . {\displaystyle \tan {\frac {\theta }{2}}={\frac {\sin \theta }{1+\cos \theta }}.\,} Also, if the numerator and denominator are both multiplied by (1 - cos θ), the result is:
tan θ 2 = 1 − cos θ sin θ . {\displaystyle \tan {\frac {\theta }{2}}={\frac {1-\cos \theta }{\sin \theta }}.\,} This also gives:
tan θ 2 = csc θ − cot θ . {\displaystyle \tan {\frac {\theta }{2}}=\csc \theta -\cot \theta .\,} Similar manipulations for the cot function give:
cot θ 2 = ± 1 + cos θ 1 − cos θ = 1 + cos θ sin θ = sin θ 1 − cos θ = csc θ + cot θ . {\displaystyle \cot {\frac {\theta }{2}}=\pm \,{\sqrt {\frac {1+\cos \theta }{1-\cos \theta }}}={\frac {1+\cos \theta }{\sin \theta }}={\frac {\sin \theta }{1-\cos \theta }}=\csc \theta +\cot \theta .\,}
If ψ {\displaystyle \psi } θ {\displaystyle \theta } ϕ {\displaystyle \phi } ψ + θ + ϕ = π = {\displaystyle \psi +\theta +\phi =\pi =}
tan ( ψ ) + tan ( θ ) + tan ( ϕ ) = tan ( ψ ) tan ( θ ) tan ( ϕ ) . {\displaystyle \tan(\psi )+\tan(\theta )+\tan(\phi )=\tan(\psi )\tan(\theta )\tan(\phi ).} Proof:[ 1]
ψ = π − θ − ϕ tan ( ψ ) = tan ( π − θ − ϕ ) = − tan ( θ + ϕ ) = − tan θ − tan ϕ 1 − tan θ tan ϕ = tan θ + tan ϕ tan θ tan ϕ − 1 ( tan θ tan ϕ − 1 ) tan ψ = tan θ + tan ϕ tan ψ tan θ tan ϕ − tan ψ = tan θ + tan ϕ tan ψ tan θ tan ϕ = tan ψ + tan θ + tan ϕ {\displaystyle {\begin{aligned}\psi &=\pi -\theta -\phi \\\tan(\psi )&=\tan(\pi -\theta -\phi )\\&=-\tan(\theta +\phi )\\&={\frac {-\tan \theta -\tan \phi }{1-\tan \theta \tan \phi }}\\&={\frac {\tan \theta +\tan \phi }{\tan \theta \tan \phi -1}}\\(\tan \theta \tan \phi -1)\tan \psi &=\tan \theta +\tan \phi \\\tan \psi \tan \theta \tan \phi -\tan \psi &=\tan \theta +\tan \phi \\\tan \psi \tan \theta \tan \phi &=\tan \psi +\tan \theta +\tan \phi \\\end{aligned}}}
Miscellaneous -- the triple cotangent identity If ψ + θ + ϕ = π 2 = {\displaystyle \psi +\theta +\phi ={\tfrac {\pi }{2}}=}
cot ( ψ ) + cot ( θ ) + cot ( ϕ ) = cot ( ψ ) cot ( θ ) cot ( ϕ ) {\displaystyle \cot(\psi )+\cot(\theta )+\cot(\phi )=\cot(\psi )\cot(\theta )\cot(\phi )} Proof:
Replace each of ψ {\displaystyle \psi } θ {\displaystyle \theta } ϕ {\displaystyle \phi }
Given
ψ + θ + ϕ = π 2 {\displaystyle \psi +\theta +\phi ={\tfrac {\pi }{2}}\,} ∴ ( π 2 − ψ ) + ( π 2 − θ ) + ( π 2 − ϕ ) = 3 π 2 − ( ψ + θ + ϕ ) = 3 π 2 − π 2 = π {\displaystyle \therefore ({\tfrac {\pi }{2}}-\psi )+({\tfrac {\pi }{2}}-\theta )+({\tfrac {\pi }{2}}-\phi )={\tfrac {3\pi }{2}}-(\psi +\theta +\phi )={\tfrac {3\pi }{2}}-{\tfrac {\pi }{2}}=\pi } so the result follows from the triple tangent identity.
Prosthaphaeresis identities sin θ ± sin ϕ = 2 sin ( θ ± ϕ 2 ) cos ( θ ∓ ϕ 2 ) {\displaystyle \sin \theta \pm \sin \phi =2\sin \left({\frac {\theta \pm \phi }{2}}\right)\cos \left({\frac {\theta \mp \phi }{2}}\right)} cos θ + cos ϕ = 2 cos ( θ + ϕ 2 ) cos ( θ − ϕ 2 ) {\displaystyle \cos \theta +\cos \phi =2\cos \left({\frac {\theta +\phi }{2}}\right)\cos \left({\frac {\theta -\phi }{2}}\right)} cos θ − cos ϕ = − 2 sin ( θ + ϕ 2 ) sin ( θ − ϕ 2 ) {\displaystyle \cos \theta -\cos \phi =-2\sin \left({\frac {\theta +\phi }{2}}\right)\sin \left({\frac {\theta -\phi }{2}}\right)}
First, start with the sum-angle identities:
sin ( α + β ) = sin α cos β + cos α sin β {\displaystyle \sin(\alpha +\beta )=\sin \alpha \cos \beta +\cos \alpha \sin \beta } sin ( α − β ) = sin α cos β − cos α sin β {\displaystyle \sin(\alpha -\beta )=\sin \alpha \cos \beta -\cos \alpha \sin \beta } By adding these together,
sin ( α + β ) + sin ( α − β ) = sin α cos β + cos α sin β + sin α cos β − cos α sin β = 2 sin α cos β {\displaystyle \sin(\alpha +\beta )+\sin(\alpha -\beta )=\sin \alpha \cos \beta +\cos \alpha \sin \beta +\sin \alpha \cos \beta -\cos \alpha \sin \beta =2\sin \alpha \cos \beta } Similarly, by subtracting the two sum-angle identities,
sin ( α + β ) − sin ( α − β ) = sin α cos β + cos α sin β − sin α cos β + cos α sin β = 2 cos α sin β {\displaystyle \sin(\alpha +\beta )-\sin(\alpha -\beta )=\sin \alpha \cos \beta +\cos \alpha \sin \beta -\sin \alpha \cos \beta +\cos \alpha \sin \beta =2\cos \alpha \sin \beta } Let α + β = θ {\displaystyle \alpha +\beta =\theta } α − β = ϕ {\displaystyle \alpha -\beta =\phi }
∴ α = θ + ϕ 2 {\displaystyle \therefore \alpha ={\frac {\theta +\phi }{2}}} β = θ − ϕ 2 {\displaystyle \beta ={\frac {\theta -\phi }{2}}} Substitute θ {\displaystyle \theta } ϕ {\displaystyle \phi }
sin θ + sin ϕ = 2 sin ( θ + ϕ 2 ) cos ( θ − ϕ 2 ) {\displaystyle \sin \theta +\sin \phi =2\sin \left({\frac {\theta +\phi }{2}}\right)\cos \left({\frac {\theta -\phi }{2}}\right)} sin θ − sin ϕ = 2 cos ( θ + ϕ 2 ) sin ( θ − ϕ 2 ) = 2 sin ( θ − ϕ 2 ) cos ( θ + ϕ 2 ) {\displaystyle \sin \theta -\sin \phi =2\cos \left({\frac {\theta +\phi }{2}}\right)\sin \left({\frac {\theta -\phi }{2}}\right)=2\sin \left({\frac {\theta -\phi }{2}}\right)\cos \left({\frac {\theta +\phi }{2}}\right)} Therefore,
sin θ ± sin ϕ = 2 sin ( θ ± ϕ 2 ) cos ( θ ∓ ϕ 2 ) {\displaystyle \sin \theta \pm \sin \phi =2\sin \left({\frac {\theta \pm \phi }{2}}\right)\cos \left({\frac {\theta \mp \phi }{2}}\right)}
Similarly for cosine, start with the sum-angle identities:
cos ( α + β ) = cos α cos β − sin α sin β {\displaystyle \cos(\alpha +\beta )=\cos \alpha \cos \beta \ -\sin \alpha \sin \beta } cos ( α − β ) = cos α cos β + sin α sin β {\displaystyle \cos(\alpha -\beta )=\cos \alpha \cos \beta +\sin \alpha \sin \beta } Again, by adding and substracting
cos ( α + β ) + cos ( α − β ) = cos α cos β − sin α sin β + cos α cos β + sin α sin β = 2 cos α cos β {\displaystyle \cos(\alpha +\beta )+\cos(\alpha -\beta )=\cos \alpha \cos \beta \ -\sin \alpha \sin \beta +\cos \alpha \cos \beta +\sin \alpha \sin \beta =2\cos \alpha \cos \beta \ } cos ( α + β ) − cos ( α − β ) = cos α cos β − sin α sin β − cos α cos β − sin α sin β = − 2 sin α sin β {\displaystyle \cos(\alpha +\beta )-\cos(\alpha -\beta )=\cos \alpha \cos \beta \ -\sin \alpha \sin \beta -\cos \alpha \cos \beta -\sin \alpha \sin \beta =-2\sin \alpha \sin \beta } Substitute θ {\displaystyle \theta } ϕ {\displaystyle \phi }
cos θ + cos ϕ = 2 cos ( θ + ϕ 2 ) cos ( θ − ϕ 2 ) {\displaystyle \cos \theta +\cos \phi =2\cos \left({\frac {\theta +\phi }{2}}\right)\cos \left({\frac {\theta -\phi }{2}}\right)} cos θ − cos ϕ = − 2 sin ( θ + ϕ 2 ) sin ( θ − ϕ 2 ) {\displaystyle \cos \theta -\cos \phi =-2\sin \left({\frac {\theta +\phi }{2}}\right)\sin \left({\frac {\theta -\phi }{2}}\right)}
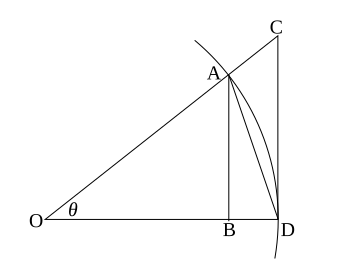
Illustration of the sine and tangent inequalities. The figure at the right shows a sector of a circle with radius 1. The sector is θ/(2π) of the whole circle, so its area is θ/2.
O A = O D = 1 {\displaystyle OA=OD=1\,} A B = sin θ {\displaystyle AB=\sin \theta \,} C D = tan θ {\displaystyle CD=\tan \theta \,} The area of triangle OAD is AB/2, or sinθ/2. The area of triangle OCD is CD/2, or tanθ/2.
Since triangle OAD lies completely inside the sector, which in turn lies completely inside triangle OCD, we have
sin θ < θ < tan θ {\displaystyle \sin \theta <\theta <\tan \theta \,} This geometric argument applies if 0<θ<π/2. It relies on definitions of arc length and area , which act as assumptions, so it is rather a condition imposed in construction of trigonometric functions than a provable property.[ 2]
sin θ θ < 1 i f 0 < θ {\displaystyle {\frac {\sin \theta }{\theta }}<1\ \ \ \mathrm {if} \ \ \ 0<\theta \,} For negative values of θ we have, by symmetry of the sine function
sin θ θ = sin ( − θ ) − θ < 1 {\displaystyle {\frac {\sin \theta }{\theta }}={\frac {\sin(-\theta )}{-\theta }}<1\,} Hence
sin θ θ < 1 i f θ ≠ 0 {\displaystyle {\frac {\sin \theta }{\theta }}<1\ \ \ \mathrm {if} \ \ \ \theta \neq 0\,} tan θ θ > 1 i f 0 < θ < π 2 {\displaystyle {\frac {\tan \theta }{\theta }}>1\ \ \ \mathrm {if} \ \ \ 0<\theta <{\frac {\pi }{2}}\,}
lim θ → 0 sin θ = 0 {\displaystyle \lim _{\theta \to 0}{\sin \theta }=0\,} lim θ → 0 cos θ = 1 {\displaystyle \lim _{\theta \to 0}{\cos \theta }=1\,}
Sine and angle ratio identity lim θ → 0 sin θ θ = 1 {\displaystyle \lim _{\theta \to 0}{\frac {\sin \theta }{\theta }}=1} Proof: From the previous inequalities, we have, for small angles
sin θ < θ < tan θ {\displaystyle \sin \theta <\theta <\tan \theta \,} Therefore,
sin θ θ < 1 < tan θ θ {\displaystyle {\frac {\sin \theta }{\theta }}<1<{\frac {\tan \theta }{\theta }}\,} Consider the right-hand inequality. Since
tan θ = sin θ cos θ {\displaystyle \tan \theta ={\frac {\sin \theta }{\cos \theta }}} ∴ 1 < sin θ θ cos θ {\displaystyle \therefore 1<{\frac {\sin \theta }{\theta \cos \theta }}} Multply through by cos θ {\displaystyle \cos \theta }
cos θ < sin θ θ {\displaystyle \cos \theta <{\frac {\sin \theta }{\theta }}} Combining with the left-hand inequality:
cos θ < sin θ θ < 1 {\displaystyle \cos \theta <{\frac {\sin \theta }{\theta }}<1} Taking cos θ {\displaystyle \cos \theta } θ → 0 {\displaystyle \theta \to 0}
lim θ → 0 cos θ = 1 {\displaystyle \lim _{\theta \to 0}{\cos \theta }=1\,} Therefore,
lim θ → 0 sin θ θ = 1 {\displaystyle \lim _{\theta \to 0}{\frac {\sin \theta }{\theta }}=1}
Cosine and angle ratio identity lim θ → 0 1 − cos θ θ = 0 {\displaystyle \lim _{\theta \to 0}{\frac {1-\cos \theta }{\theta }}=0} Proof:
1 − cos θ θ = 1 − cos 2 θ θ ( 1 + cos θ ) = sin 2 θ θ ( 1 + cos θ ) = ( sin θ θ ) × sin θ × ( 1 1 + cos θ ) {\displaystyle {\begin{aligned}{\frac {1-\cos \theta }{\theta }}&={\frac {1-\cos ^{2}\theta }{\theta (1+\cos \theta )}}\\&={\frac {\sin ^{2}\theta }{\theta (1+\cos \theta )}}\\&=\left({\frac {\sin \theta }{\theta }}\right)\times \sin \theta \times \left({\frac {1}{1+\cos \theta }}\right)\\\end{aligned}}} The limits of those three quantities are 1, 0, and 1/2, so the resultant limit is zero.
Cosine and square of angle ratio identity lim θ → 0 1 − cos θ θ 2 = 1 2 {\displaystyle \lim _{\theta \to 0}{\frac {1-\cos \theta }{\theta ^{2}}}={\frac {1}{2}}} Proof:
As in the preceding proof,
1 − cos θ θ 2 = sin θ θ × sin θ θ × 1 1 + cos θ . {\displaystyle {\frac {1-\cos \theta }{\theta ^{2}}}={\frac {\sin \theta }{\theta }}\times {\frac {\sin \theta }{\theta }}\times {\frac {1}{1+\cos \theta }}.\,} The limits of those three quantities are 1, 1, and 1/2, so the resultant limit is 1/2.
Proof of Compositions of trig and inverse trig functions All these functions follow from the Pythagorean trigonometric identity. We can prove for instance the function
sin [ arctan ( x ) ] = x 1 + x 2 {\displaystyle \sin[\arctan(x)]={\frac {x}{\sqrt {1+x^{2}}}}} Proof:
We start from
sin 2 θ + cos 2 θ = 1 {\displaystyle \sin ^{2}\theta +\cos ^{2}\theta =1} Then we divide this equation by cos 2 θ {\displaystyle \cos ^{2}\theta }
cos 2 θ = 1 tan 2 θ + 1 {\displaystyle \cos ^{2}\theta ={\frac {1}{\tan ^{2}\theta +1}}} Then use the substitution θ = arctan ( x ) {\displaystyle \theta =\arctan(x)}
1 − sin 2 [ arctan ( x ) ] = 1 tan 2 [ arctan ( x ) ] + 1 {\displaystyle 1-\sin ^{2}[\arctan(x)]={\frac {1}{\tan ^{2}[\arctan(x)]+1}}} Then we use the identity tan [ arctan ( x ) ] ≡ x {\displaystyle \tan[\arctan(x)]\equiv x}
sin [ arctan ( x ) ] = x x 2 + 1 {\displaystyle \sin[\arctan(x)]={\frac {x}{\sqrt {x^{2}+1}}}}
E. T. Whittaker and G. N. Watson. A course of modern analysis , Cambridge University Press, 1952 ↑ "संग्रहीत प्रति" . मूल से 29 अक्तूबर 2013 को पुरालेखित. अभिगमन तिथि 8 जून 2014 .↑ Richman, Fred (March 1993). . "A Circular Argument" . The College Mathematics Journal . 24 (2): 160–162. डीओआइ :10.2307/2686787 . मूल से 17 मार्च 2016 को पुरालेखित . अभिगमन तिथि 3 नवम्बर 2012 . 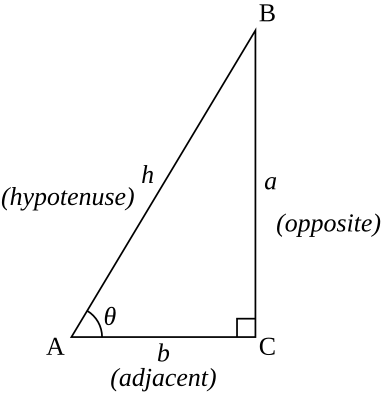





















































































































































![{\displaystyle \sin[\arctan(x)]={\frac {x}{\sqrt {1+x^{2}}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7d3ed8cedb4c73b01b65314a15152647c9000086)




![{\displaystyle 1-\sin ^{2}[\arctan(x)]={\frac {1}{\tan ^{2}[\arctan(x)]+1}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d0bb45d076e27715801c0437e364d4b1f45dfb1a)
![{\displaystyle \tan[\arctan(x)]\equiv x}](https://wikimedia.org/api/rest_v1/media/math/render/svg/49ce3dc146ff12eb2efb89a4388afcb984b7da8e)
![{\displaystyle \sin[\arctan(x)]={\frac {x}{\sqrt {x^{2}+1}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5c5222bb21dc2d342d1363c855694bae8b967914)