यहाँ कुछ प्रमुख गुणनफल दिये गये हैं जिनके प्रयोग से गुणनखण्ड एवं अन्य कार्यों में बहुत सुविधा होती है।
उभयनिष्ट गुणक का चित्रात्मक निरूपण c ( a + b ) = c a + c b {\displaystyle c(a+b)=ca+cb\,} उदाहरण 3 x ( 4 x + 6 y ) = 12 x 2 + 18 x y {\displaystyle 3x(4x+6y)=12x^{2}+18xy\,}
द्विपद के वर्ग का चित्रात्मक निरूपण ( a + b ) 2 = a 2 + 2 a b + b 2 {\displaystyle (a+b)^{2}=a^{2}+2ab+b^{2}\,} त्रिपदी व्यंजक : a 2 + 2 a b + b 2 {\displaystyle a^{2}+2ab+b^{2}\;} पूर्ण वर्ग त्रिपद कहलाता है।
इसी प्रकार,
( a − b ) 2 = a 2 − 2 a b + b 2 {\displaystyle (a-b)^{2}=a^{2}-2ab+b^{2}\,} उदाहरण ( 2 x − 3 y ) 2 = ( 2 x ) 2 + 2 ( 2 x ) ( − 3 y ) + ( − 3 y ) 2 {\displaystyle (2x-3y)^{2}=(2x)^{2}+2(2x)(-3y)+(-3y)^{2}\,} सरल करने पर:
( 2 x − 3 y ) 2 = 4 x 2 − 12 x y + 9 y 2 {\displaystyle (2x-3y)^{2}=4x^{2}-12xy+9y^{2}\,}
चित्रात्मक निरूपण ( x + a ) ( x + b ) = x 2 + ( a + b ) x + a b {\displaystyle (x+a)(x+b)=x^{2}+(a+b)x+ab\,} उदाहरण ( 3 x + 4 ) ( 3 x − 7 ) = ( 3 x ) ( 3 x ) + ( 3 x ) ( − 7 ) + ( 3 x ) ( 4 ) + ( 4 ) ( − 7 ) {\displaystyle (3x+4)(3x-7)=(3x)(3x)+(3x)(-7)+(3x)(4)+(4)(-7)\,} पदों को एकत्र करने पर:
( 3 x + 4 ) ( 3 x − 7 ) = 9 x 2 − 21 x + 12 x − 28 {\displaystyle (3x+4)(3x-7)=9x^{2}-21x+12x-28\,} या:
( 3 x + 4 ) ( 3 x − 7 ) = 9 x 2 − 9 x − 28 {\displaystyle (3x+4)(3x-7)=9x^{2}-9x-28\,}
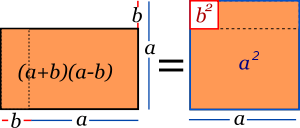
'द्विपद युग्म' का गुणनफल ( a + b ) ( a − b ) = a 2 − b 2 {\displaystyle (a+b)(a-b)=a^{2}-b^{2}\,} उदाहरण ( 3 x + 5 y ) ( 3 x − 5 y ) = {\displaystyle (3x+5y)(3x-5y)=\,} ( 3 x ) ( 3 x ) + ( 3 x ) ( − 5 y ) + ( 5 y ) ( 3 x ) + ( 5 y ) ( − 5 y ) {\displaystyle (3x)(3x)+(3x)(-5y)+(5y)(3x)+(5y)(-5y)\,} पदों को एकत्र करने पर:
( 3 x + 5 y ) ( 3 x − 5 y ) = 9 x 2 − 25 y 2 {\displaystyle (3x+5y)(3x-5y)=9x^{2}-25y^{2}\,}
एक त्रिपद के वर्ग का चित्रात्मक निरूपण ( a + b + c ) 2 = a 2 + b 2 + c 2 + 2 ( a b + a c + b c ) {\displaystyle (a+b+c)^{2}=a^{2}+b^{2}+c^{2}+2(ab+ac+bc)\,} ( a + b + c + d ) 2 = a 2 + b 2 + c 2 + d 2 + 2 ( a b + a c + a d + b c + b d + c d ) {\displaystyle (a+b+c+d)^{2}=a^{2}+b^{2}+c^{2}+d^{2}+2(ab+ac+ad+bc+bd+cd)\,} उदाहरण ( 3 x + 2 y − 5 z ) 2 = ( 3 x + 2 y − 5 z ) ( 3 x + 2 y − 5 z ) {\displaystyle (3x+2y-5z)^{2}=(3x+2y-5z)(3x+2y-5z)\,} गुणा करने पर:
( 3 x + 2 y − 5 z ) 2 = 3 x ⋅ 3 x + 3 x ⋅ 2 y + 3 x ⋅ ( − 5 z ) {\displaystyle (3x+2y-5z)^{2}=3x\cdot 3x+3x\cdot 2y+3x\cdot (-5z)\,} + 2 y ⋅ 3 x + 2 y ⋅ 2 y + 2 y ⋅ ( − 5 z ) {\displaystyle +2y\cdot 3x+2y\cdot 2y+2y\cdot (-5z)\,} + ( − 5 z ) ⋅ 3 x + ( − 5 z ) ⋅ 2 y + ( − 5 z ) ⋅ ( − 5 z ) {\displaystyle +(-5z)\cdot 3x+(-5z)\cdot 2y+(-5z)\cdot (-5z)\,} पदों को एकत्र करने के बाद:
( 3 x + 2 y − 5 z ) 2 = 9 x 2 + 4 y 2 + 25 z 2 + 2 ( 6 x y − 15 x z − 10 y z ) {\displaystyle (3x+2y-5z)^{2}=9x^{2}+4y^{2}+25z^{2}+2(6xy-15xz-10yz)\,} या:
( 3 x + 2 y − 5 z ) 2 = 9 x 2 + 4 y 2 + 25 z 2 + 12 x y − 30 x z − 20 y z {\displaystyle (3x+2y-5z)^{2}=9x^{2}+4y^{2}+25z^{2}+12xy-30xz-20yz\,}
द्विपद के घन का आयतनों के योग के रूप में चित्रण ( a + b ) 3 = a 3 + 3 a 2 b + 3 a b 2 + b 3 {\displaystyle (a+b)^{3}=a^{3}+3a^{2}b+3ab^{2}+b^{3}\,} काशी (Cauchy) सर्वसमिका:
( a + b ) 3 = a 3 + b 3 + 3 a b ( a + b ) {\displaystyle (a+b)^{3}=a^{3}+b^{3}+3ab(a+b)\,} उदाहरण ( x + 2 y ) 3 = x 3 + 3 ( x ) 2 ( 2 y ) + 3 ( x ) ( 2 y ) 2 + ( 2 y ) 3 {\displaystyle (x+2y)^{3}=x^{3}+3(x)^{2}(2y)+3(x)(2y)^{2}+(2y)^{3}\,} पदों का समूह बनाने के बाद:
( x + 2 y ) 3 = x 3 + 6 x 2 y + 12 x y 2 + 8 y 3 {\displaystyle (x+2y)^{3}=x^{3}+6x^{2}y+12xy^{2}+8y^{3}\,} इसी प्रकार,
( a − b ) 3 = a 3 − 3 a 2 b + 3 a b 2 − b 3 {\displaystyle (a-b)^{3}=a^{3}-3a^{2}b+3ab^{2}-b^{3}\,} काशी (Cauchy) सर्वसमिका:
( a − b ) 3 = a 3 − b 3 − 3 a b ( a − b ) {\displaystyle (a-b)^{3}=a^{3}-b^{3}-3ab(a-b)\,} उदाहरण ( x − 2 y ) 3 = x 3 − 3 ( x ) 2 ( 2 y ) + 3 ( x ) ( 2 y ) 2 − ( 2 y ) 3 {\displaystyle (x-2y)^{3}=x^{3}-3(x)^{2}(2y)+3(x)(2y)^{2}-(2y)^{3}\,} पदों का समूह बनाने के बाद:
( x − 2 y ) 3 = x 3 − 6 x 2 y + 12 x y 2 − 8 y 3 {\displaystyle (x-2y)^{3}=x^{3}-6x^{2}y+12xy^{2}-8y^{3}\,}
( x 2 + x + 1 ) ( x 2 − x + 1 ) = x 4 + x 2 + 1 {\displaystyle (x^{2}+x+1)(x^{2}-x+1)=x^{4}+x^{2}+1\,}
a 3 + b 3 + c 3 − 3 a b c = ( a + b + c ) ( a 2 + b 2 + c 2 − a b − b c − a c ) {\displaystyle a^{3}+b^{3}+c^{3}-3abc=(a+b+c)(a^{2}+b^{2}+c^{2}-ab-bc-ac)\,} a 3 + b 3 + c 3 − 3 a b c = 1 2 ( a + b + c ) [ ( a − b ) 2 + ( b − c ) 2 + ( a − c ) 2 ] {\displaystyle a^{3}+b^{3}+c^{3}-3abc={\frac {1}{2}}(a+b+c)[(a-b)^{2}+(b-c)^{2}+(a-c)^{2}]\,}
( a + b ) 2 + ( a − b ) 2 = 2 ( a 2 + b 2 ) {\displaystyle (a+b)^{2}+(a-b)^{2}=2(a^{2}+b^{2})\,} ( a + b ) 2 − ( a − b ) 2 = 4 a b {\displaystyle (a+b)^{2}-(a-b)^{2}=4ab\,} ( a + b ) 4 − ( a − b ) 4 = 8 a b ( a 2 + b 2 ) {\displaystyle (a+b)^{4}-(a-b)^{4}=8ab(a^{2}+b^{2})\,}
( a 2 + b 2 ) ( x 2 + y 2 ) = ( a x + b y ) 2 + ( a y − b x ) 2 {\displaystyle (a^{2}+b^{2})(x^{2}+y^{2})=(ax+by)^{2}+(ay-bx)^{2}\,} ( a 2 + b 2 + c 2 ) ( x 2 + y 2 + z 2 ) = ( a x + b y + c z ) 2 + ( a y − b x ) 2 + ( a z − c x ) 2 + ( b z − c y ) 2 {\displaystyle (a^{2}+b^{2}+c^{2})(x^{2}+y^{2}+z^{2})=(ax+by+cz)^{2}+(ay-bx)^{2}+(az-cx)^{2}+(bz-cy)^{2}\,}
घनों का योग a 3 + b 3 = ( a + b ) ( a 2 − a b + b 2 ) {\displaystyle a^{3}+b^{3}=(a+b)(a^{2}-ab+b^{2})\,} घनों का अन्तर a 3 − b 3 = ( a − b ) ( a 2 + a b + b 2 ) {\displaystyle a^{3}-b^{3}=(a-b)(a^{2}+ab+b^{2})\,} n वें घातों का योगयदि और केवल यदि "n" विषम संख्या हो तो, a n + b n = ( a + b ) ( a n − 1 − a n − 2 b + a n − 3 b 2 − ⋯ + b n − 1 ) {\displaystyle a^{n}+b^{n}=(a+b)(a^{n-1}-a^{n-2}b+a^{n-3}b^{2}-\cdots +b^{n-1})\,} n वें घातों का अन्तरa n − b n = ( a − b ) ( a n − 1 + a n − 2 b + a n − 3 b 2 + ⋯ + b n − 1 ) {\displaystyle a^{n}-b^{n}=(a-b)(a^{n-1}+a^{n-2}b+a^{n-3}b^{2}+\cdots +b^{n-1})\,} निम्नलिखित सूत्र किसी घन को दो वर्गों के अन्तर के रूप में अभिव्यक्त करता है-
a 3 = ( ( a + 1 ) a 2 ) 2 − ( ( a − 1 ) a 2 ) 2 {\displaystyle a^{3}=\left({\frac {(a+1)a}{2}}\right)^{2}-\left({\frac {(a-1)a}{2}}\right)^{2}}
साँचा:Lien BA






































![{\displaystyle a^{3}+b^{3}+c^{3}-3abc={\frac {1}{2}}(a+b+c)[(a-b)^{2}+(b-c)^{2}+(a-c)^{2}]\,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c861b04d0eb0a8d7e5f8bec4a258a7d9665049b4)









